记录一下自己实现二分查找算法的过程和实验结果,二分查找算法细节请自行百度。
Golang 二分查找算法实验(单元压力测试)
Golang版本信息
go version go1.13.5 windows/amd64
记录一下自己实现二分查找算法的过程和实验结果,二分查找算法细节请自行百度。
1. 生成随机有序数组
这里生成随机有序数组不考虑是否有重复的数字,实现过程很简单,就是生成随机数字并压入数组中。
func generateNums(size int) []int {
// 参数是数组的大小
var nums []int
rand.Seed(time.Now().UnixNano())
for i := 0; i < size; i++ {
nums = append(nums, rand.Intn(size))
}
sort.Ints(nums)
return nums
}
2. 二分查找算法
使用通道传递查找次数结果,参数分别为,数组,目的数字。
func binarySearch(nums []int, targetNum int) int64 {
var low, high int
var t int64
high = len(nums) - 1
for low <= high {
t++
mid := (low + high) / 2
guess := nums[mid]
if guess == targetNum {
return t
}
if guess > targetNum {
high = mid - 1
} else {
low = mid + 1
}
}
return t
}
3. 使用单元测试调用
这里定义测试数组大小固定为204800000,即204800000个数字,所以最大搜索次数是25,最小是1。使用b *testing.B中的b.N来循环进行测试
// 初始化 - 以便测试数据相同
var (
size = 204800000
nums []int
)
func init() {
nums = generateNums(size)
}
初始化数据后,创建两个测试实例,分别使用goroutine和不使用goroutine的情况
// 使用goroutine
func BenchmarkBinarySearch(b *testing.B) {
var (
averT int64
wg sync.WaitGroup
)
wg.Add(b.N)
for i := 0; i < b.N; i++ {
targetNum := nums[rand.Intn(size)]
go func(targetNum int) {
defer wg.Done()
number := binarySearch(nums, targetNum)
atomic.AddInt64(&averT, number)
}(targetNum)
}
wg.Wait()
log.Printf("总共测试%d次,平均每次搜索%v次", b.N, int(averT)/b.N)
}
// 不使用goroutine
func BenchmarkBinarySearchWithNoGoroutine(b *testing.B) {
var averT int64
for t := 0; t < b.N; t++ {
targetNum := nums[rand.Intn(size)]
runNumber := binarySearch(nums, targetNum)
averT += runNumber
}
log.Printf("总共测试%d次,平均每次搜索%v次", b.N, int(averT)/b.N)
}
4. 实验结果
以下均为Golang的Benchmark压力测试生成的随机结果。
4.1 多Goroutine搜索
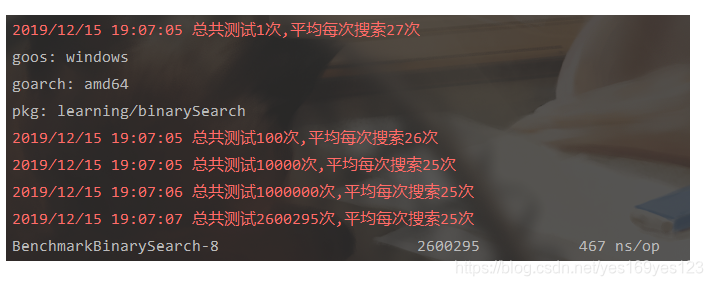
共循环搜索2600295次,平均每执行一次流程耗费467纳秒
| 程序执行次数 | 平均搜索次数 |
|---|---|
| 1 | 27 |
| 10k | 26 |
| 100k | 25 |
| 260k(2600295) | 25 |
控制台结果:
4.2 普通搜索
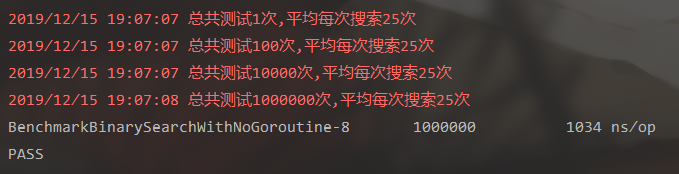
共循环搜索100k次,平均每执行一次流程耗费1034纳秒
| 程序执行次数 | 平均搜索次数 |
|---|---|
| 1 | 25 |
| 100 | 25 |
| 10k | 25 |
| 100k | 25 |
控制台结果:
5. 实验结论
压力测试一共运行了4次程序,但是普通搜索很明显比创建Goroutine慢,而且压力测试根据普通搜索能承受的压力将次数减至100k次。根据二分查找时间复杂度计算公式可以得知二分查找的时间上限为 $\log_2{N} +1$,所以平均每次搜索次数都正确。
证明二分查找时间为对数时间。
实验可以进一步优化,对于如此庞大的数组,应该传指针而不是传值,传值影响运行速度。